Rのロジスティック回帰

データサイエンスと統計では、従属変数の結果がTrue / False、Yes / No、0/1などのカテゴリ値になる場合は回帰モデルです。 通常、ロジスティック回帰モデルは二項です。 ただし、拡張することはできます。 イベントの成功または失敗の確率を、数式に基づく従属変数として測定します。 この方程式は、従属変数（応答変数）を独立変数（予測変数）に関連付けます。

ロジスティック回帰は線形回帰の一般化された形式であると言えますが、主な違いは予測値の範囲が（-∞、∞）であるのに対し、ロジスティック回帰の予測値の範囲は（0,1）です。 この投稿では、ロジスティック回帰と、それをRプログラミング言語で実装する方法について学習します。

ロジスティック回帰を使用する理由

独立変数（予測変数）と従属変数（応答変数）の関係を理解し​​た後、線形回帰がよく使用されます。 従属変数がカテゴリ型の場合は、ロジスティック回帰を選択することをお勧めします。 これは最も単純なモデルの1つですが、解釈が簡単で実装が高速であるため、さまざまなアプリケーションで非常に役立ちます。

ロジスティック回帰では、データ/観測値を個別のクラスに分類しようとします。これは、ロジスティック回帰が分類アルゴリズムであることを示しています。 ロジスティック回帰は、次のようなさまざまなアプリケーションで役立ちます。

顧客の信用記録と銀行残高を使用して、顧客が銀行から融資を受ける資格があるかどうかを予測できます（応答変数は「適格」または「不適格」になります。上記の条件からアクセスできます。応答変数は2つの値しか持てませんが、線形回帰では、従属変数はより連続的な複数の値を取ることができます。

Ubuntu20.04でのRのロジスティック回帰

Rでは、応答変数がバイナリの場合、イベントの値を予測するのに最適なのは、ロジスティック回帰モデルを使用することです。 このモデルは、メソッドを使用して次の方程式を見つけます。

Xjはj番目の予測変数であり、βjはXjの係数推定値です。 ロジスティック回帰モデルでは、方程式を使用して確率を計算し、値1の観測値/出力を生成します。つまり、確率が0.5以上の出力は、値1と見なされます。それ以外の場合は、すべての値が考慮されます。 0として。

次のステップバイステップの例では、Rでロジスティック回帰を使用する方法を説明します。

ステップ1：モデルのデータをRにロードする
まず、モデルの使用法を示すためにデフォルトのデータセットをロードする必要があります。 このデータセットは、以下に示すように1000個の観測値で構成されています。

このデータセット列では、デフォルトは個人がデフォルトであるかどうかを示しています。 学生は、個人が学生であるかどうかを示しています。 バランスは、個人の平均バランスを示しています。 そして収入は個人の収入を示しています。 回帰モデルを構築するために、ステータス、銀行残高、および収入を使用して、個人がデフォルトになる確率を予測します。

ステップ2：トレーニングとテストサンプルの作成
データセットをテストセットとトレーニングセットに分割して、モデルをテストおよびトレーニングします。

データの70％はトレーニングセットに使用され、30％はテストセットに使用されます。

ステップ3：ロジスティック回帰のフィッティング
Rでは、ロジスティック回帰を適合させるために、glm関数を使用し、ファミリを二項に設定する必要があります。

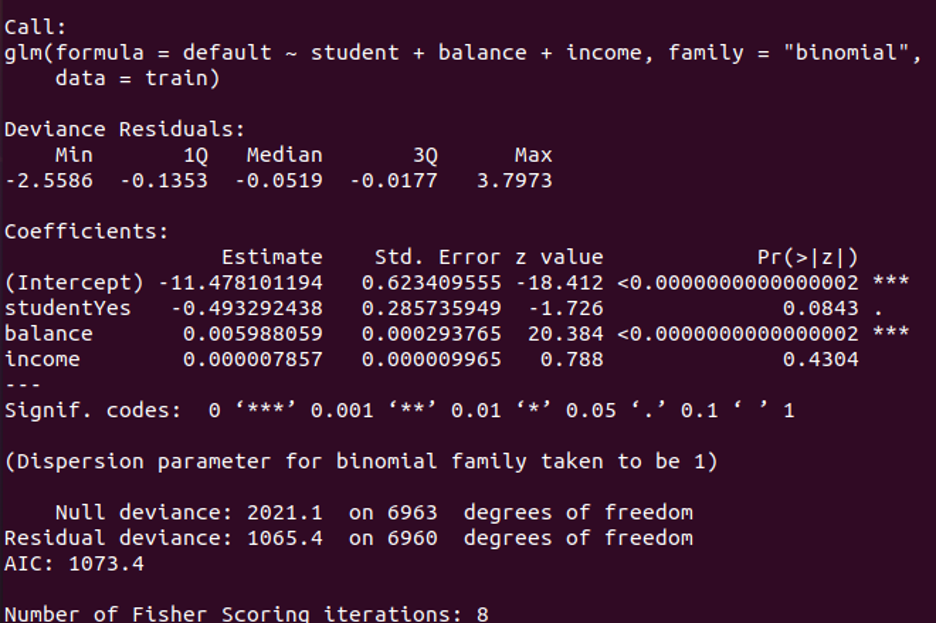
対数オッズでは、平均変化は係数で示されます。 学生のステータスのP値は0.0843です。残高のP値は<0.0000、収入のP値は0.4304です。 これらの値は、各独立変数がデフォルトの可能性を予測するのにどれほど効果的であるかを示しています。

Rでは、ロジスティックモデルがデータにどの程度適合しているかを確認します マクファデンズ、R2 メトリックが使用されます。 範囲は0〜1です。値が0に近い場合は、モデルが適合していないことを示します。 ただし、0.40を超える値は適合モデルと見なされます。 pR2関数を使用して計算できます マクファデンのR2。

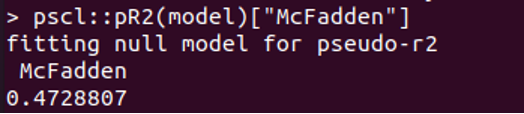
上記の値は0.472を超えているため、モデルが適合しているだけでなく、モデルの予測力が高いことを示しています。

関数の重要性は、varImp関数を使用して計算することもできます。 値が高いほど、その変数の重要性が他の変数よりも高くなることを示します。

ステップ4：ロジスティック回帰モデルを使用して予測を行う
回帰モデルを適合させた後、個人がバランス、収入、および学生のステータスのさまざまな値でデフォルトになるかどうかについて予測することはできません。

ご覧のとおり、残高が1400の場合、収入は2000で、学生のステータスは「はい」で、デフォルトの確率は0.02732106です。 一方、同じパラメータを持っているが学生ステータスが「いいえ」の個人は、デフォルトの確率が0.0439です。

データセット内のすべての個人を計算するには、次のコードを使用します。

ステップ5：ロジスティック回帰モデルの診断：
この最後のステップでは、テストデータベースでモデルのパフォーマンスを分析します。 デフォルトでは、確率が0.5を超える個人は「デフォルト」と予測されます。 ただし、 optimalCutoff（） 関数は、モデルの精度を最大化します。

上で見ることができるように、 0.5451712は 最適な確率カットオフ。 したがって、0.5451712の確率が「デフォルト」以上である個人は、「デフォルト」と見なされます。 ただし、個人の確率が0.5451712未満の場合は、「デフォルトではない」と見なされます。

結論

このチュートリアルを終えると、Ubuntu20.04のRプログラミング言語でのロジスティック回帰に精通しているはずです。 また、このモデルをいつ使用する必要があるのか​​、および二項値でそれが重要である理由を特定することもできます。 コードと方程式の助けを借りて、Rでロジスティック回帰を使用する5つのステップを、例を使用して詳細に説明するために実装しました。 これらの手順は、データのRへのロード、データセットのトレーニングとテスト、モデルのフィッティング、モデル診断への予測作成から始まるすべてをカバーしています。