これ 論文 もともと公開された ビルトイン EricKleppenによる。
分散は、データ分析と機械学習で使用される強力な統計です。 これは、範囲、四分位範囲(IQR)および標準偏差。 分散を理解することは、データの広がりを洞察し、サンプルグループの違いを比較したり、重要なモデリング機能を特定したりするために使用できるため、重要です。 分散は、トレーニングデータのさまざまなサンプルを使用することによるモデルのパフォーマンスの変化を理解するために、機械学習でも使用されます。
Pythonを使用すると、分散の計算が簡単になります。 Pythonコードに飛び込む前に、まず分散とは何か、そしてそれを計算する方法について説明します。 このチュートリアルを終了すると、Pythonを使用して分散を計算するためのいくつかの方法とともに、分散が重要な統計である理由をよりよく理解できるようになります。
分散とは何ですか?
最高の価格で最高の体験
ニュースレターにサインアップして、TNW Conference 2023のチケットがいつ発売されるかを最初に知ってください!
分散は、分散を測定する統計です。 分散が小さい場合は、値が一般的に類似しており、平均から大きく変化しないことを示します。分散が大きい場合は、値が平均からより広く分散していることを示します。 計算では特定のセット内のすべてのデータポイントが取り込まれるため、サンプルセットまたは母集団全体のいずれかで分散を使用できます。 標本と母集団を比較すると計算はわずかに異なりますが、分散は平均からの差の2乗の平均として計算できます。
分散は二乗値であるため、標準偏差などの他の変動性の尺度と比較して解釈が難しい場合があります。 とにかく、差異を確認することは役立つ場合があります。 そうすることで、どちらを決定するのが簡単になります 統計的検定 データで使用します。 統計的検定によっては、サンプル間の不均一な分散が発生する可能性があります 斜め また バイアス 結果。
人気のあるものの1つ 統計的検定 分散分析を適用する分散分析(ANOVA)テストと呼ばれます。 ANOVA検定は、カテゴリ独立変数と量的従属変数を分析するときに、グループ平均のいずれかが互いに有意に異なるかどうかを測定するために使用されます。 たとえば、ソーシャルメディアの使用が睡眠時間に影響を与えるかどうかを分析したいとします。 ソーシャルメディアの使用を低使用、中使用、高使用などのさまざまなカテゴリに分類し、ANOVAテストを実行して、グループ平均間に統計的差異があるかどうかを判断できます。 テストは、結果がグループの違いまたは個人の違いによって説明されるかどうかを示すことができます。
差異をどのように見つけますか?
データセットの分散の計算は、セットが母集団全体であるか、母集団のサンプルであるかによって異なる場合があります。
母集団全体の分散を計算する式は次のようになります。
σ²=∑(Xᵢ—μ)²/ N
式の説明:
- σ²=母分散
- Σ=合計…
- Χᵢ=各値
- μ=母平均
- Ν=母集団の値の数
- 数値の範囲の例を使用して、計算を段階的に見ていきましょう。
数字の範囲の例:8、6、12、3、13、9
母平均(μ)を求めます。
各値から平均を差し引くことにより、平均からの偏差を計算します。

各偏差を2乗して、正の数を取得します。

二乗値を合計します。

二乗和をNまたはn-1で割ります。
母集団全体を処理しているので、Nで除算します。母集団のサンプルを処理している場合は、n-1で除算します。
69.5 / 6 = 11.583
あります! 私たちの人口の分散は11.583です。
サンプル分散を計算するときにn-1を使用するのはなぜですか?
式にn-1を適用すると、 ベッセルの訂正、フリードリヒ・ベッセルにちなんで名付けられました。 サンプルを使用する場合、母集団の推定分散を計算する必要があります。 サンプルにn-1の代わりにNを使用した場合、推定値にバイアスがかかり、母分散を過小評価する可能性があります。 n-1を使用すると、分散推定が大きくなり、サンプルの変動が過大評価されるため、バイアスが減少します。
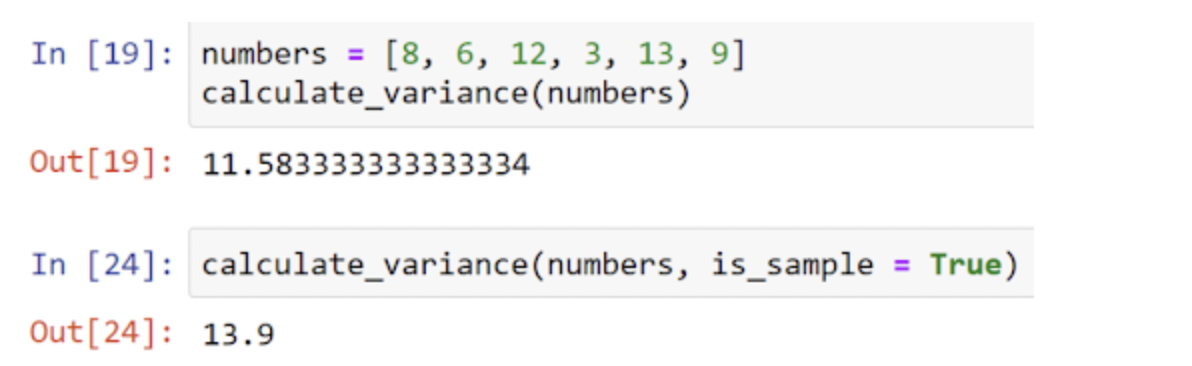
値がサンプルからのものであると偽って分散を再計算してみましょう。

ご覧のとおり、分散が大きくなっています。
Pythonを使用した分散の計算
手作業で計算を行ったので、大量の値のセットに対して計算を完了するのは非常に面倒であることがわかります。 幸い、Pythonは非常に大きなデータの計算を簡単に処理できます。 Pythonを使用して2つの方法を検討します。
- 独自の分散計算関数を作成する
- Pandasの組み込み関数を使用する
分散関数の記述
分散を計算する関数を書き始めるとき、手動で計算するときに行った手順を思い出してください。 関数が2つのパラメーターを受け取るようにします。
- 人口:数字の配列
- is_sample:サンプルと母集団のどちらで作業しているかに応じて計算を変更するブール値
2つのパラメーターを受け取る関数を定義することから始めます。

次に、母平均を計算するロジックを追加します。

平均を計算した後、各値の平均からの差を見つけます。 リスト内包表記を使用して、これを1行で行うことができます。

次に、差を二乗して合計します。

最後に、分散を計算します。 If / Elseステートメントを使用すると、is_sampleparameterを利用できます。 is_sampleがtrueの場合、(n-1)を使用して分散を計算します。 false(デフォルト)の場合は、Nを使用します。
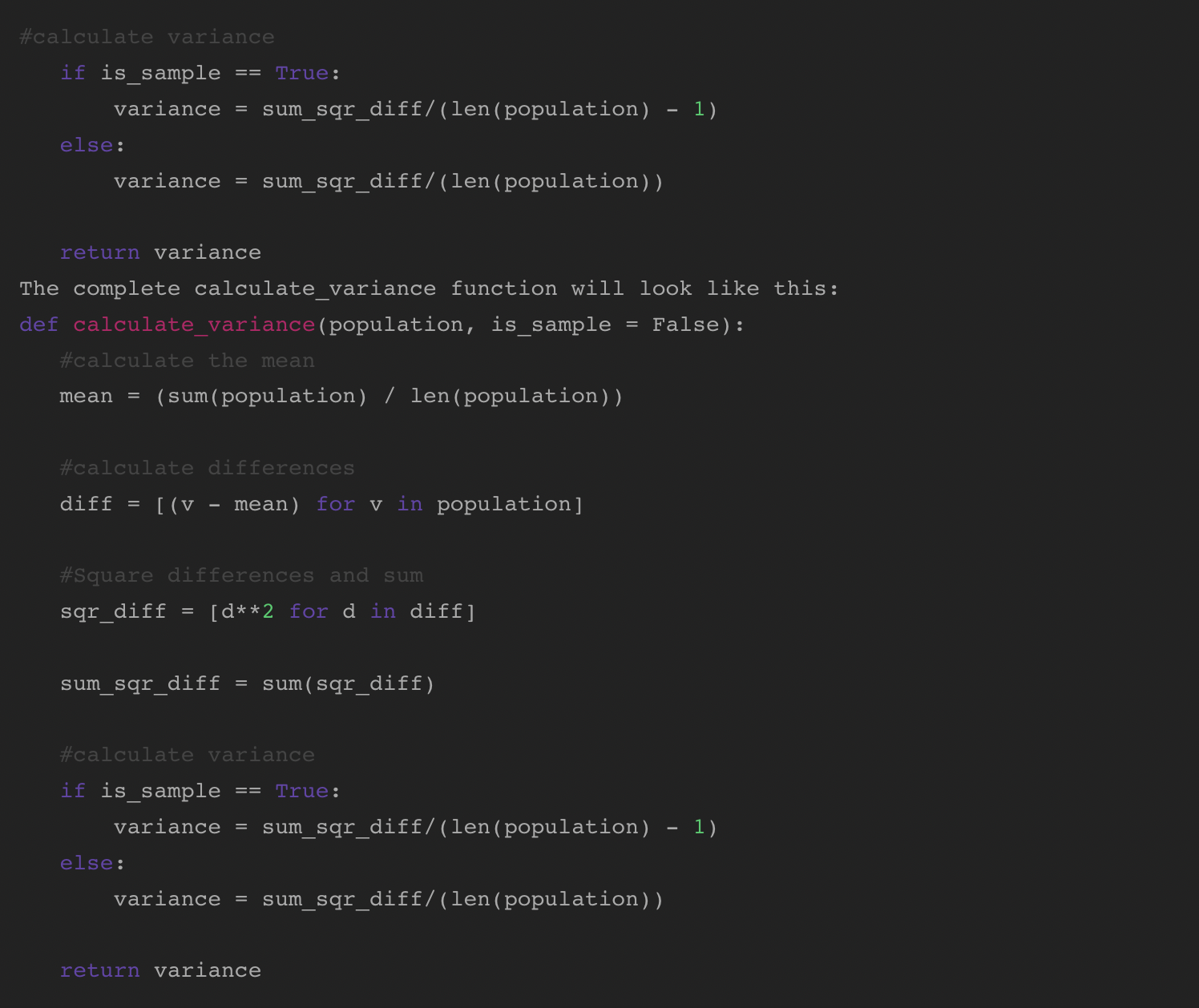
手作業で計算した数値の範囲を使用して、計算をテストできます。
パンダを使用して分散を見つける
10行未満のコードで分散を計算する関数を記述できますが、分散を見つけるさらに簡単な方法があります。 Pandasを使用すると、1行のコードでそれを行うことができます。 いくつかのデータをロードして、分散を見つける実際の例を見てみましょう。
サンプルデータの読み込み
パンダの例では、 BMW価格チャレンジ 無料でダウンロードできるKaggleのデータセット。 まず、Pandasライブラリをインポートしてから、CSVファイルをPandasデータフレームに読み込みます。

データセットの行数をカウントし、最初の5行を表示して、すべてが正しく読み込まれたことを確認できます。
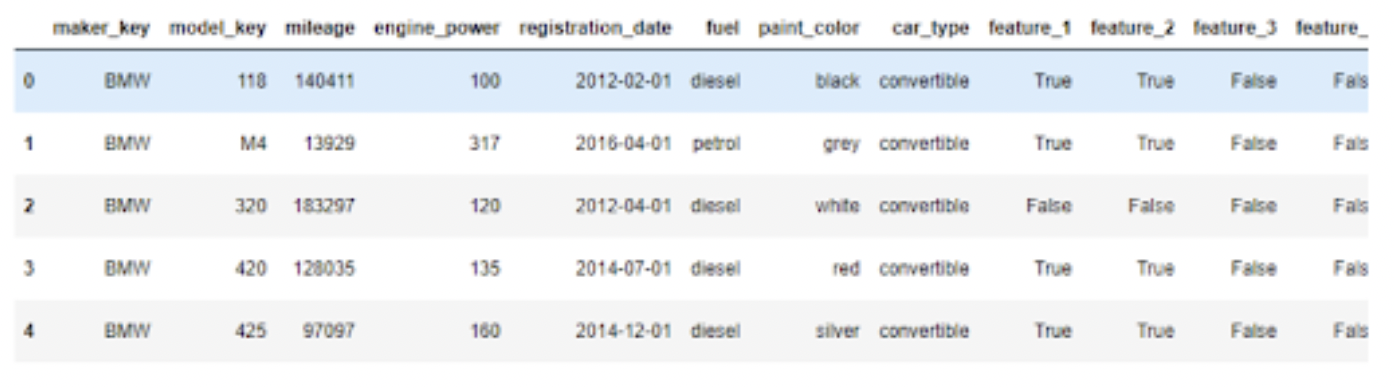
BMWデータの分散を見つける
BMWのデータセットは4843行であるため、手動で計算するのは面白くありません。 代わりに、データフレームの列をcalculate_variance関数にプラグインして、分散を返すことができます。 数値列mileage、engine_power、およびpriceの分散を見つけましょう。
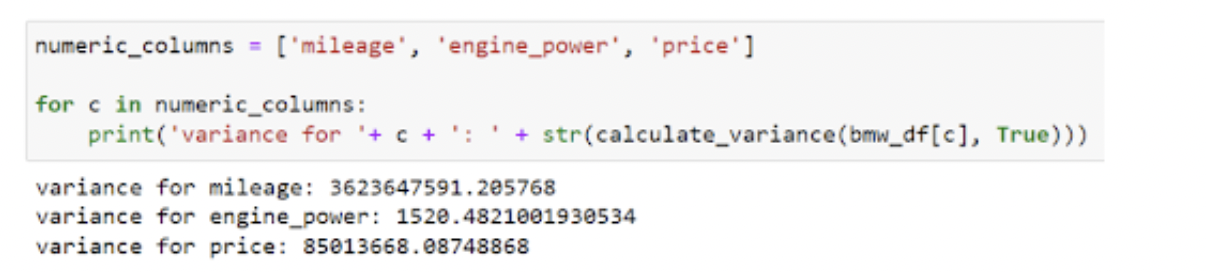
Pandas var()関数の使用
分散の計算を忘れて独自の関数を記述できない場合に備えて、Pandasにはvar()という名前の分散を計算するための組み込み関数があります。 デフォルトでは、サンプル母集団を想定し、計算にn-1を使用します。 ただし、ddof=0引数を渡すことで計算を調整できます。
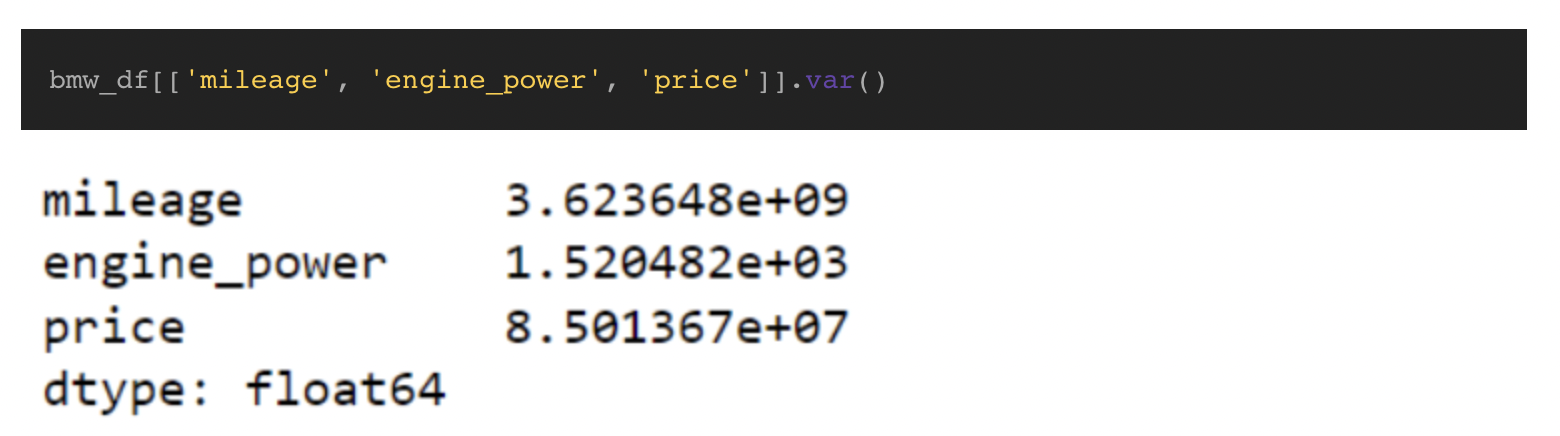
ご覧のとおり、Var()関数はcalculate_variance関数によって生成された値と一致し、コードは1行だけです。 結果を確認すると、マイレージの分散が大きく、値が平均と大きく異なる傾向があることがわかります。 人が運転する必要のある距離には多くの要因が関係しているため、これは理にかなっています。 比較すると、engine_powerの分散は低く、値が平均から大きく変化しないことを示しています。
持ち帰り
分散を理解することは、グループの違いを評価するために使用できるため、データ分析と機械学習の重要な部分になる可能性があります。 分散は、どの統計的検定がデータ主導の意思決定に役立つかにも影響します。 分散が大きいとは、値が平均から大きく分散していることを意味しますが、分散が小さいと、数値が平均から大きく分散していないことを意味します。 値のセットが少ない場合は、5つのステップで手作業で分散を計算することができます。 大規模なデータセットの場合、PythonとPandasを使用して分散を計算するのがいかに簡単であるかを確認しました。 PandasのVar()関数は、データフレーム内の数値列の分散を1行のコードで計算します。これは非常に便利です。
The post Pythonを使用して分散を見つける方法 appeared first on Gamingsym Japan.
