もっと詳しく
この記事では、MATLAB diff() 関数について知っておく必要があるすべてのことを説明します。

この関数を実装して、行列のベクトル要素、行、および列の違いを見つける方法を見ていきます。 この記事では、数学関数の近似導関数を取得する方法も学習します。

これは、多次元でさまざまなタイプのベクトルと配列を使用してこの関数を使用するさまざまな方法を示すコードフラグメントと画像を使用した実用的な例を通して示されます。

MATLAB diff 関数の構文

MATLAB diff 関数の説明

diff() 関数は、1 つの要素と入力ベクトルまたは行列 “x” のテキストとの差を “d” に返します。 配列を入力として diff を呼び出すと、次元に沿って操作します。 したがって、「d」の結果は、操作対象の次元で n-1 要素の次元のサイズ n の配列になります。 操作したい次元は、入力「dim」を使用して選択されます。 入力「n」は、導関数の次数を設定する整数スカラーです。 この関数は、「x」でベクトル、2D、および多次元配列を受け入れますが、入力「n」および「dim」は正の整数スカラー型です。 ベクトルとさまざまな行列タイプを使用したこの関数の実用的な例を以下に示します。

例 1: MATLAB 関数 diff() を使用してベクトルの隣接する要素間の差を取得する方法

ここで、MATLAB 関数 diff を使用して、ベクトル「v」の隣接する要素間の差を見つける方法を見てみましょう。 これを行うには、スクリプトを作成し、次のコードを記述します。

v = [ 1, 2, 4, 7, 11, 7, 4, 2, 1 ];
r = 差分 ( v )

スクリプトの最初の行で、9 要素のベクトル「v」を作成します。 次に、コードの 2 行目で diff() 関数を呼び出し、入力引数として「v」を渡します。 この場合、ベクトルを送信しているため、入力「dim」は使用されません。

次の図からわかるように、MATLAB 環境のコマンド コンソールは、「d」の出力が「v」の接続された要素間の差のベクトルであることを示しています。 出力ベクトルには、入力ベクトルよりも要素が 1 つ少ないことがわかります。

例 2: 「dim」入力を使用して、MATLAB の diff() 関数で異なる次元に沿って操作する方法

異なる次元の「dim」入力を使用してこの関数を操作する場合、diff() は 2 番目の入力引数に「n」を使用するため、「n」入力を空にしないでください。 この入力を使用しない場合は、代わりに 1 を送信する必要があります。これがデフォルト値です。

例 3: 「dim」入力を使用して、MATLAB diff 関数で最初の次元に沿って操作する方法

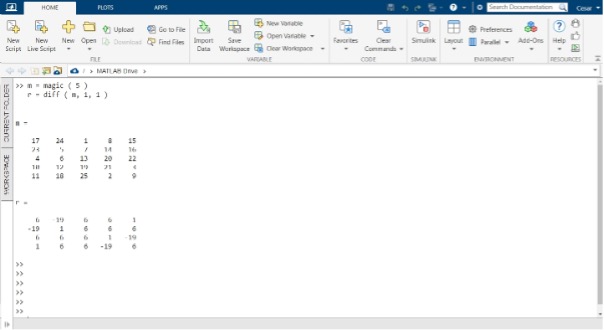
ここで、MATLAB 関数 diff を使用して、行列 “m” の列または次元 1 に沿って隣接する要素間の差を見つける方法を見てみましょう。この目的のために、スクリプトを作成し、次のコードを記述します。

スクリプトの最初の行では、magic() 関数を使用して、5 x 5 要素の配列で構成される魔方陣を作成します。 コードの 2 行目では、diff() 関数を呼び出し、入力引数として「m」を送信し、次元 1 に沿って動作することを「dim」入力で指定します。

次の図は、結果が「d」のコマンド コンソールを示しています。 この場合、「m」の次元 1 に沿って隣接する要素間の差がある 5 列 x 4 行の配列です。

例 4: 「dim」入力を使用して、MATLAB diff 関数で 2 番目の次元に沿って操作する方法

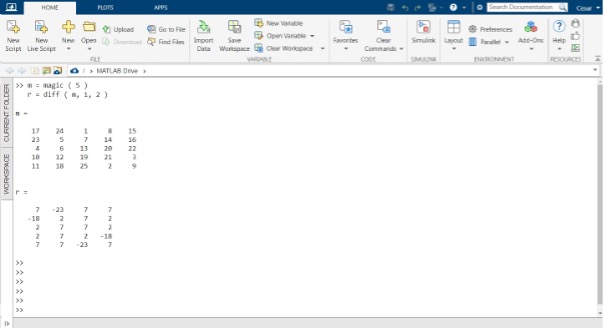
この例では、行列の次元 2、つまり行に沿って操作する方法を説明します。 これを行うには、前の例と同じコード フラグメントを使用しますが、今回は「dim」と入力して、次元 2 または魔方陣の行に沿って動作することを示します。

次の図は、結果が「d」のコマンド コンソールを示しています。 この場合、これは、「m」の次元 2 に沿って隣接する要素間の差がある 4 行 x 5 列の配列です。

例 5: MATLAB diff() を使用して関数で近似導関数を取得する方法

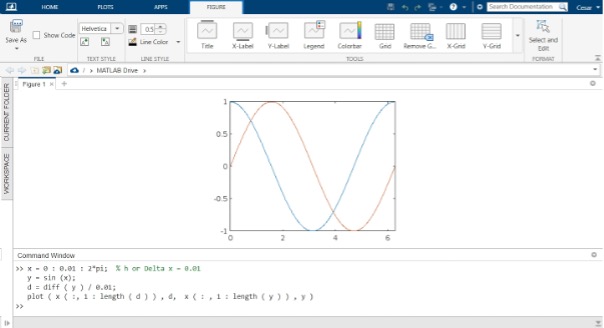
この例では、diff() 関数を使用して正弦波のおおよその導関数を取得する方法を示します。この関数を使用して、間隔 x、x+h における y の差を取得し、それを間隔で割ります。 h. 次に、この例のコードとスクリプトを見ていきます。

×＝ 0 : 0.01 : 2*円周率; % h またはデルタ x = 0.01

y = 罪 (バツ);
d = 差分 ( y ) / 0.01;
プロット ( バツ ( :, 1 : 長さ ( d ) ) 、d、x ( : , 1 : 長さ ( y ) ) 、y )

前のコード スニペットでは、最初に 0 から 2*pi までの時間ベクトル “x” を “h” で 0.01 の間隔で作成します。 次に、「x」のサインでベクトル「y」を作成して、それらが同じサイズになるようにします。 Wave が作成されたら、diff() 関数を使用して、出力「d」のベクトル「y」の要素間の差を取得します。 次に、「d」の差を「h」で割り、「y」の導関数を持つベクトルを取得します。 説明で述べたように、diff() 出力ベクトルのサイズは、入力ベクトルより n-1 要素大きく、これは、この関数が入力「n」を介して再帰的に適用されるたびに発生するため、「x」、および「 d」は対応サイズがなくなります。 波動とその導関数を表現したい場合、「d」のサイズは「x」のサイズと互換性がありません。 したがって、コードの最後の行に示されているように、「d」のサイズで定義する必要があります。 以下に、正弦「y」とその近似導関数「d」を示します。

結論

この MATLAB 記事では、MATLAB diff 関数を使用して、行列またはベクトルの隣接する要素間の違いを見つける方法について説明しました。 このリソースの使用方法を理解するのに役立つように、各モードのコード フラグメントと画像、およびこの機能が機能するさまざまな次元の実用的な例を作成しました。 関数の構造、入力引数と出力引数、および diff() が受け入れるデータ型の説明も見てきました。 この MATLAB 記事がお役に立てば幸いです。 その他のヒントや情報については、Linux Hint の他の記事を参照してください。

The post MATLAB の diff 関数 appeared first on Gamingsym Japan.