今回は、「微分とはそもそも何なのか」についての説明です。
1.初めに
中学高校の数学で微分というものを習ったかと思います。
微分とは、一次関数や二次関数などのある点の傾き(変化の割合)を求めることを指します。
何を言っているのかわかりづらいかもですが、言葉の説明ではこれ以上言いようがないのです。
ということで、次項から例を使って説明していきます。
2.ある点の傾きとは?
まず、一次関数のy=2xについて考えてみましょう。
X=1の時はy=2、x=2の時はy=4、x=3の時はy=6と変化していくので、xが1増加したらyが2増加するという関係はy=2xという直線上で変わることはありません。
この変化量が傾きです。
傾き=yの増加量÷xの増加量ということですね。
なので、y=2xの場合の傾きは2となります。
言い換えると、y=2xを微分した結果は2となります。
次は二次関数のy=x2について考えてみます。
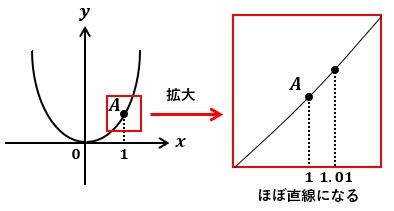
二次関数は一次関数とは違って曲線なので、ある点の傾きと言われてもピンとこないかもしれません。
なので、図1の点Aを拡大してみます。
すると、点A付近は直線に見えますよね?
この状態で一次関数の時同様に変化量を求めれば傾きが算出できます。
傾き=yの増加量÷xの増加量なので、x=1.00の地点からx=1.01までの変化量について考えてみます。
計算をすると、(1.012-1.02)÷(1.01-1.0)=2.01となります。
つまり、点Aの傾きは大体2です。
このように、ある点の傾きに関しては気長に変化量を調べれば大体の値を求めることが可能です。
…何度も大体と言ったのには理由があり、この方法では二次関数のある点の傾きを正確に算出することができません。
いくら直線に見えても実際は曲線ですからね。
そこで、正確な傾きを算出する為に微分という考え方が出てくるわけです。
3.正確な傾きを証明する
微分の話に移行する前に、正確な傾き(変化量)の証明をしておこうと思います。
y=x2の関係において、x=2の時の傾きについて考えてみます。
x=2の点B(2,4)からx軸方向にa離れた点Cがあります。

点Cの座標は(2+a,(2+a)2)となるので、点B~点C間の傾きを計算すると図2右側のようになります。
これで点B~点C間の傾きは4+aだとわかりました。
点B~点C間の距離を限りなく0に近づければ点Bの傾きが求められるので、a=0だと考えて点Bにおける傾きは4だと証明することができました。
では、y=x2上のある点の傾き、つまり座標が(x,x2)の点Dの傾きも同様に求めてみましょう。
点Dからx軸方向にh離れた点Eについて考えます。

点Eの座標は(x+h,(x+h)2)となるので、点D~点E間の傾きを計算すると図3右側のようになります。
これで点D~点E間の傾きは2x+hだとわかりました。
点D~点E間の距離hを限りなく0に近づければ点Dの傾きが求められるので、h=0だと考えて点Dにおける傾きは2xだと証明することができました。
つまり、y=x2の微分した結果は2xになります。
4.改めて微分という言葉について考えてみる
さて、ここで”微分”という言葉について考えてみましょう。
唐突になんだと思うかもしれませんが、記憶に定着させる為には必要なプロセスです。
“微分”の”微”は”ものすごく小さい”という意味です。
微小・微生物などの単語からも連想できるかと思います。
“分”はそのままで”分ける”という意味ですよね。
ということは、“微分”は”非常に小さく細かく分けること”を意味します。
ここで微分の手順を思い出して欲しいのですが、傾きを求める為に点と点の距離を限りなく小さく分けて考えていましたよね?
つまり、傾きを求めるということは”微分”という言葉通りのことを実施していただけだったんです。
5.日常生活と微分
『微分の意味はわかったけど結局日常生活で使わないから必要ないのでは?』と思う方がいるかもしれません。
ですが、普段私達が意識していないだけで身の回りは微分で溢れています。
例を挙げますね。
義務教育で「みはじ」か「はじき」と習ったことがあるのではないでしょうか?
道のりをx[m]、速さをv[m/s]、時間をt[s]とすると、道のり=速さ×時間の関係からx=vtと表せます。
つまり、一次関数で表せるんですね。
ということは、縦軸を道のりx[m]で横軸を速さv[m/s]とすれば時間t[s]が傾きになり、縦軸を道のりx[m]で横軸を時間t[s]とすれば速さv[m/s]が傾きになります。
それぞれ微分するとこの結果を導き出すことが可能です。
質量m[kg]の物体がx個あったら総質量がM[kg]になるといった単純な関係もM=mxと表せるので微分可能です。
以上のように、一次関数や二次関数で表せる関係には微分が適用できますので、普段意識していないだけで至る所に微分の概念は存在するんです。
6.学校の数学で習う微分
ここまでの長々とした説明(これでも要点以外はすっ飛ばした)で微分とは傾きを求めることだということがふんわりと理解できたと思います。
ですが、学校で習う数学の微分でこんな過程について習ったかと言うと私は記憶にありません(笑)
※ 記憶に無いだけで習っている可能性。
なので、次は実際の微分のやり方について説明していきます。
以上、「微分とはそもそも何なのか」についての説明でした。
【基礎から学ぶ微分】
